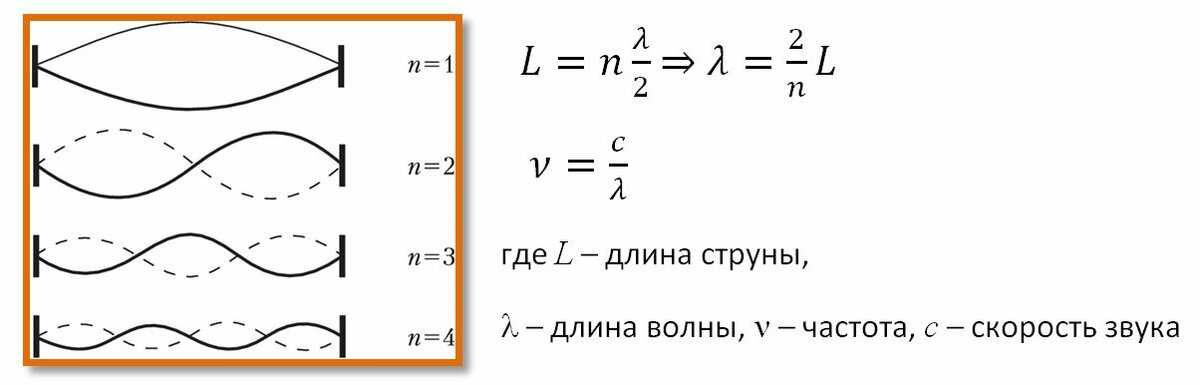Слайды и текст этой презентации
![]()
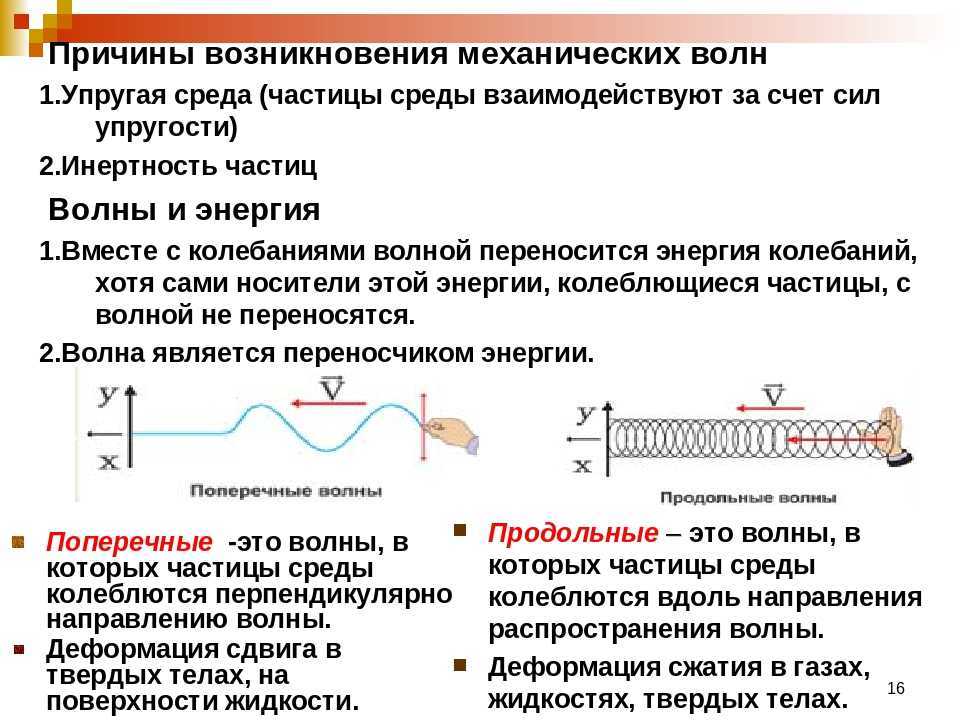
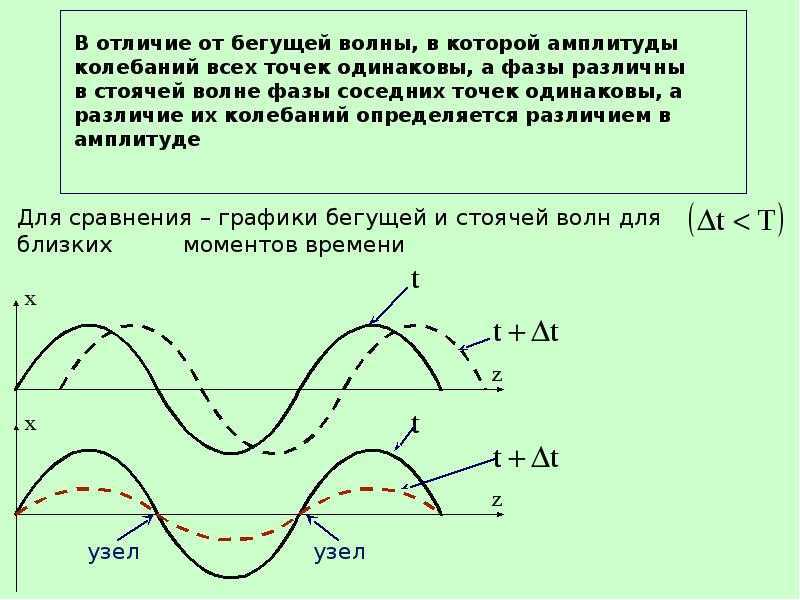
Стоячие волны
Урок физики в 10 классе(естественно-научный профиль) Автор Богданова Ирина Викторовна
![]()
Бегущие волны
![]()
Образование стоячих волн
Посмотрите на рисунок, который представляет последовательность фаз движения волн во времени (время течет сверху вниз). Синяя волна движется вправо, зеленая влево, красная волна является суммирующей и показывает, что происходит при столкновении двух волн (по научной терминологии — при наложении). Отмечены положения (узлы/nodes), в которых обе движущиеся волны нейтрализуют друг друга, и другие зоны (пучности/antinodes), в которых происходит сложение волн, и колебания обладают максимальной амплитудой.
![]()
Определение стоячей волны
Стоячая волна образуется при наложении двух бегущих навстречу гармонических волн одинаковой частоты, амплитуды и поляризации.
![]()
Как движется каждая точка стоячей волны в шнуре
Совершает синхронно со всеми остальными точками гармонические колебанияКолеблется перпендикулярно длине покоящегося шнураКолеблется с периодом равным периоду внешнего возмущенияИмеет собственную амплитуду колебаний
![]()
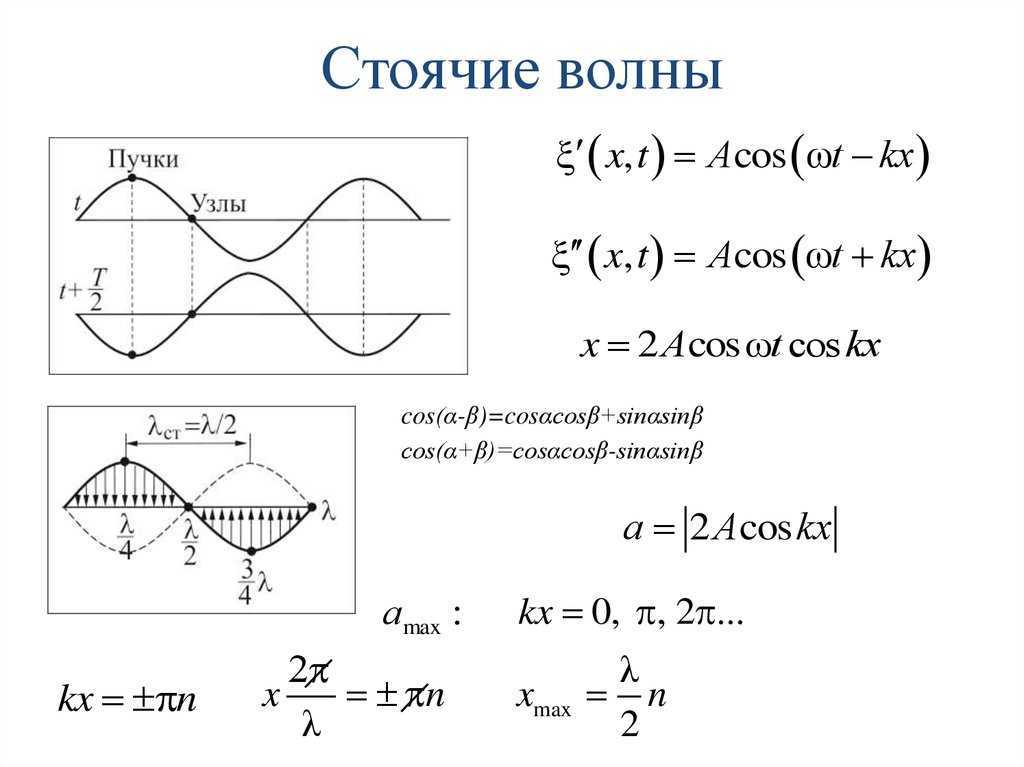
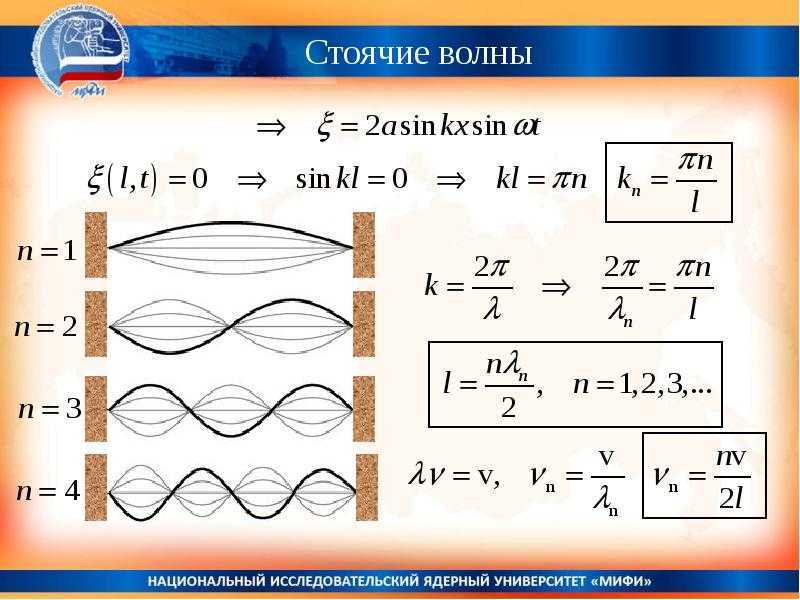
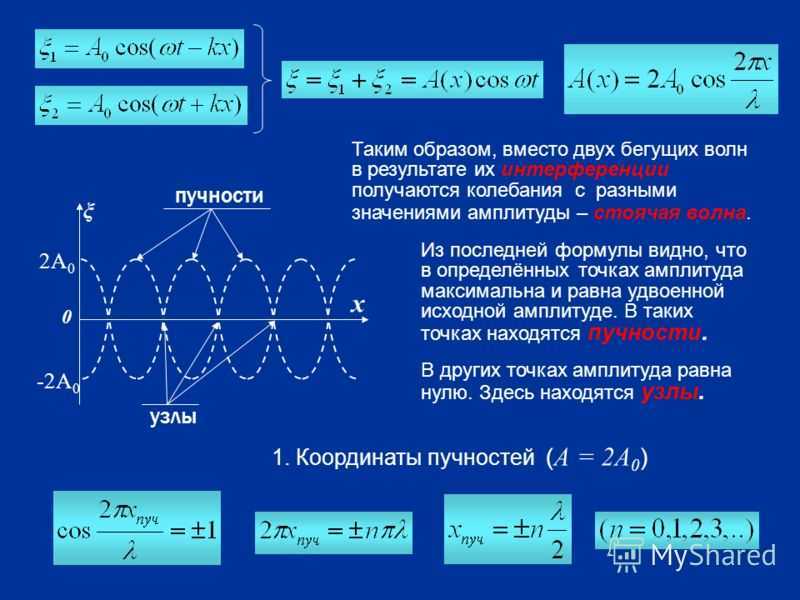
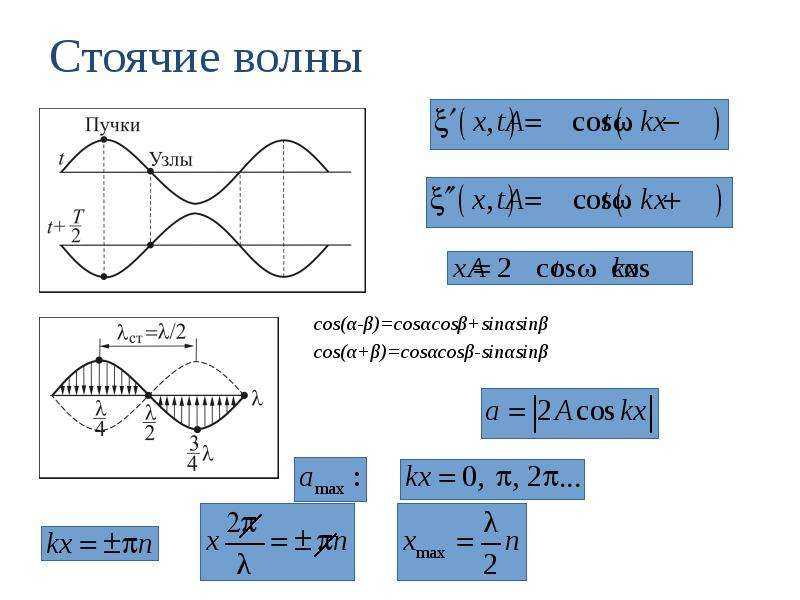
Уравнение стоячей волны
![]()
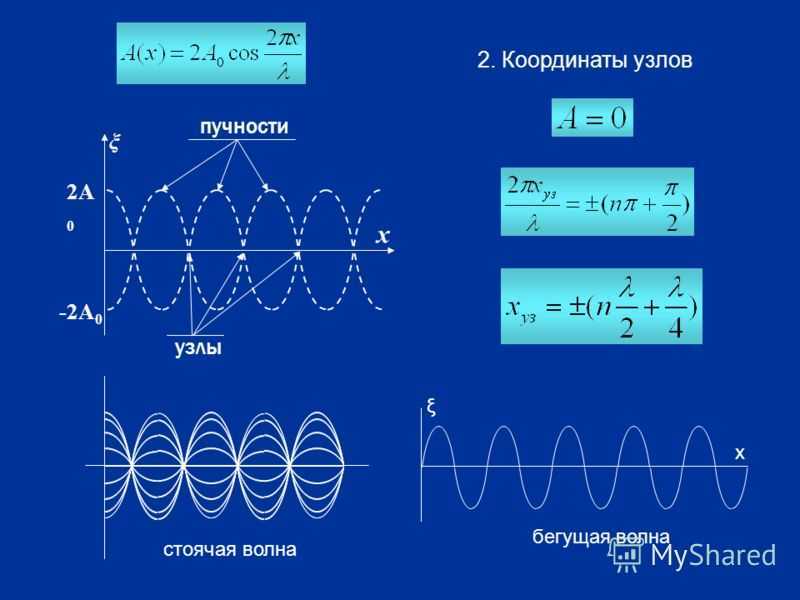
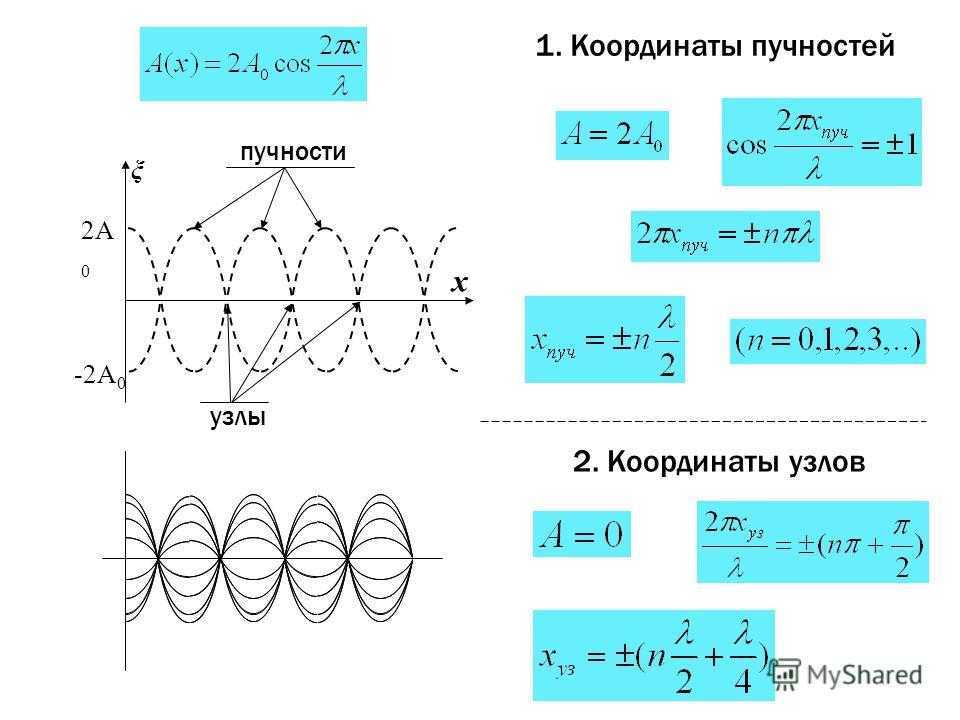
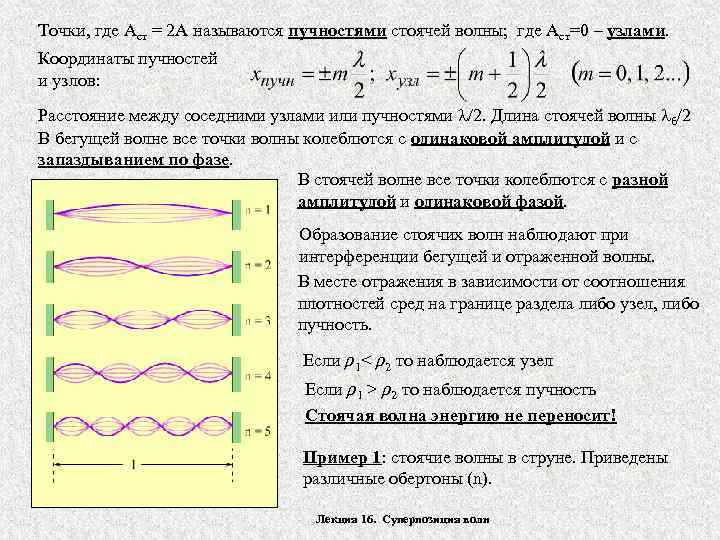
Узлы и пучности стоячей волны
Узлы – неперемещающиеся точки стоячей волныПучности – точки стоячей волны, колеблющиеся с максимальной амплитудой
![]()
![]()
Координаты
узлов и пучностей
![]()
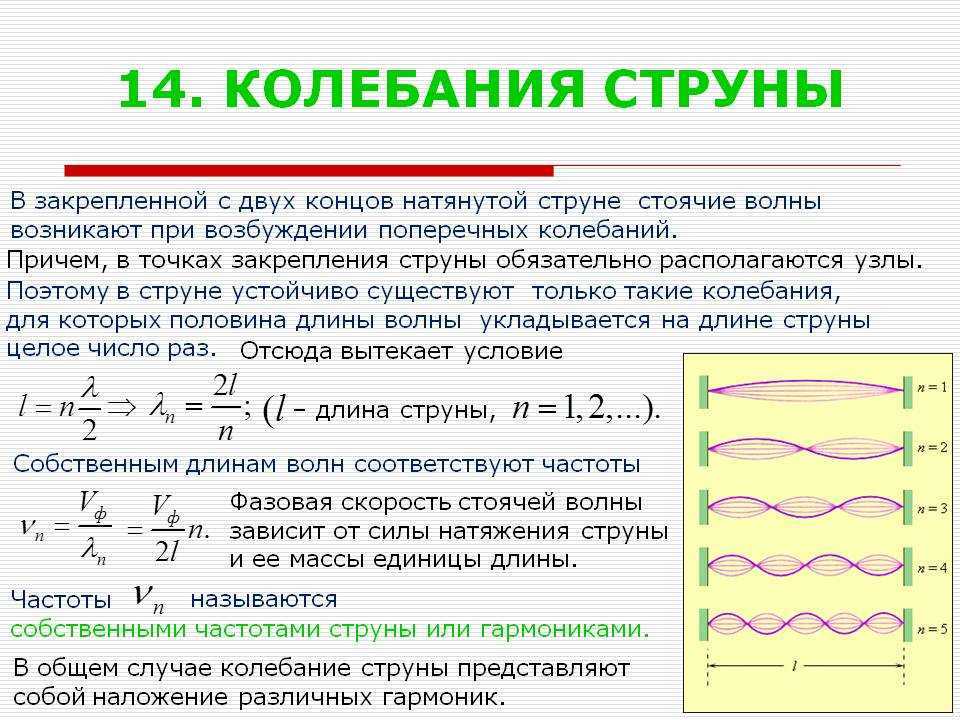
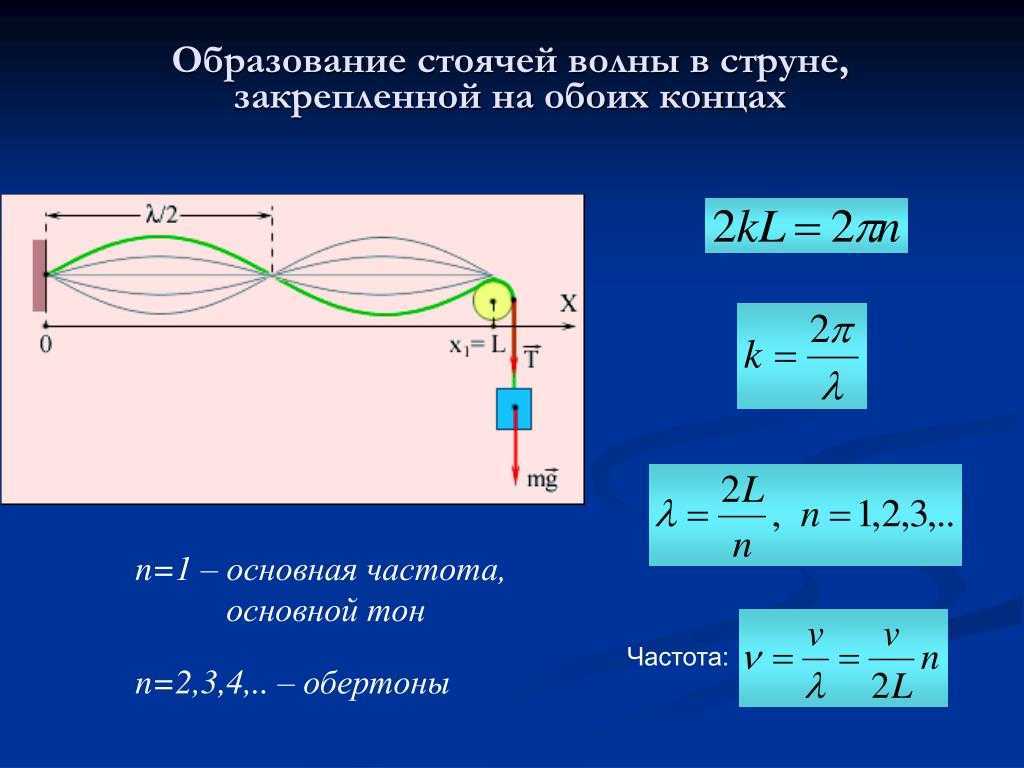
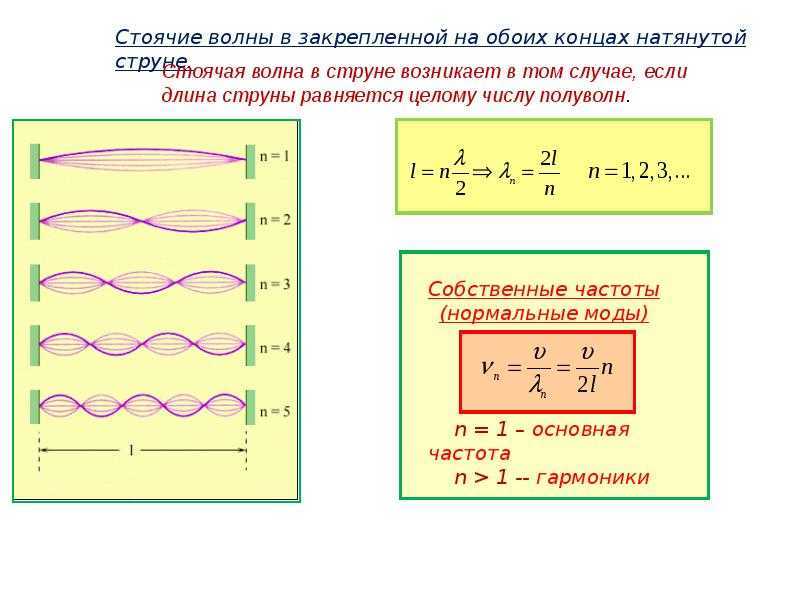
Стоячие волны в струнах
Если механическая волна, распространяющаяся в среде, встречает на своем пути какое-либо препятствие, то она может резко изменить характер своего поведения. Например, на границе раздела двух сред с разными механическими свойствами волна частично отражается, а частично проникает во вторую среду. Волна, бегущая по резиновому жгуту или струне отражается от неподвижно закрепленного конца; при этом появляется волна, бегущая во встречном направлении. В струне, закрепленной на обоих концах, возникают сложные колебания, которые можно рассматривать как результат наложения (суперпозиции) двух волн, распространяющихся в противоположных направлениях и испытывающих отражения и переотражения на концах. Колебания струн, закрепленных на обоих концах, создают звуки всех струнных музыкальных инструментов.
![]()
Струнные музыкальные инструменты
![]()
Стоячие волны в воздушных столбах
Трубка Кундта является простым приспособлением для демонстрации стоячих звуковых волн. Трубка Кундта представляет собой длинную стеклянную трубку, в которой насыпано немного легкого порошка (например пробковой пыли). Один конец трубки запаян, в другом с помощью пробки укреплен медный стержень. Если потереть стержень наканифоленной замшей, то он начнет скрипеть, а пыль расположится аккуратными кучками вдоль трубки. Такое распределение обусловлено стоячими звуковыми волнами.
![]()
Духовые музыкальные инструменты
![]()
Условие возникновения стоячих волн в шнуре
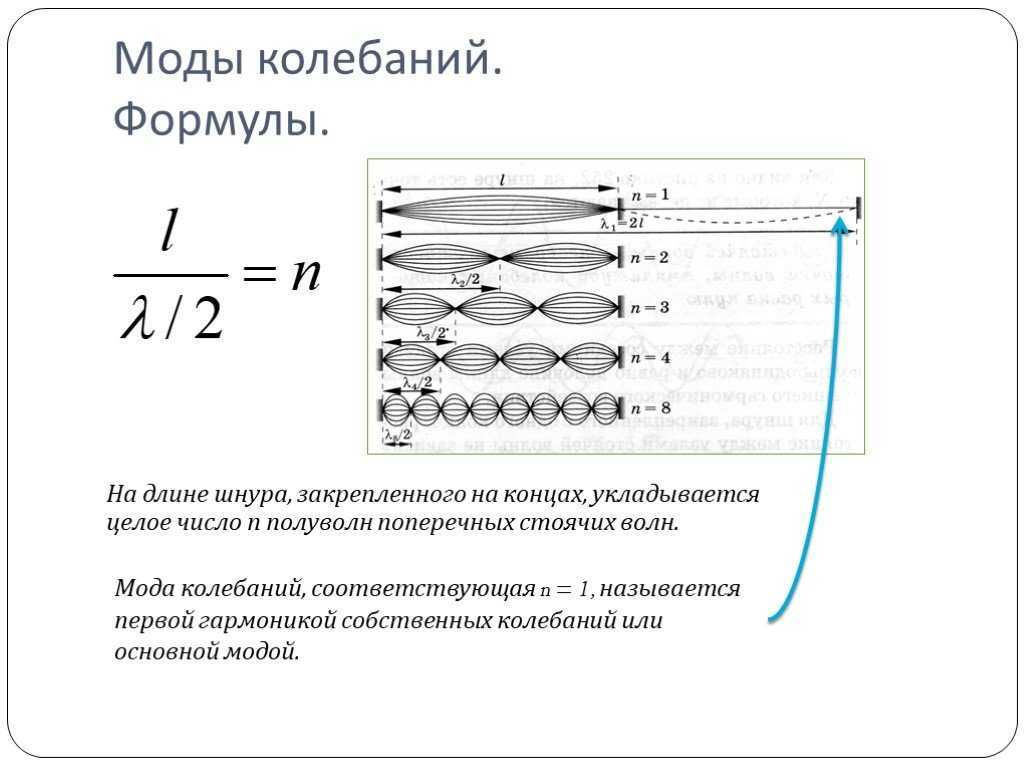
На длине шнура, закрепленного на концах, укладывается целое число полуволн поперечных стоячих волн.
![]()
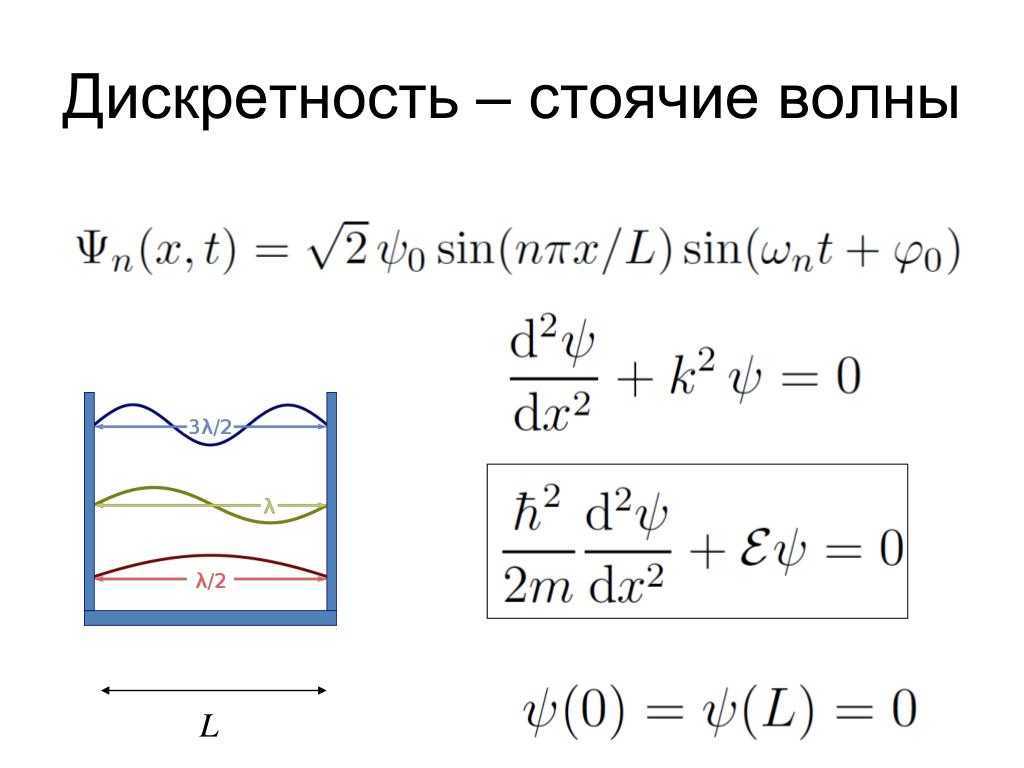
Моды колебаний
в струнах
в воздушных столбах
![]()
Частота собственных колебаний струны
n=1 – основная мода (первая гармоника)n>1 – n-ая гармоника (n-ый обертон)
У струны имеется целый набор собственных частот, кратных наиболее низкой частоте.
![]()
Тембр звука
Одной из причин того, почему разные инструменты обладают различным тембром, является то, что обертоны, сопровождающие основное колебание, выражены у разных инструментов в неодинаковой степени. Другие причины различия тембра связаны с устройством корпуса самого инструмента – его формой, размерами, жесткостью и т.п.
![]()
Ответьте на вопросы:
Какая волна называется стоячей?Объясните процесс образования стоячей волны.Охарактеризуйте особенности колебаний точки в поперечной стоячей волне.Сформулируйте определение пучностей и узлов стоячей волны.При каком условии в струне, закрепленной на концах, образуются стоячие волны?Что такое первая гармоника собственных колебаний в струне и обертоны?
![]()
Урок оконченВсем спасибо
Использованные ресурсы:Статья Джо Вулфи «Струны, стоячие волны и гармоники» http://newt.phys.unsw.edu.au/~jw/strings.html.
Примеры
Один простой пример для понимания стоячих волн — это два человека, которые трясут один конец скакалка. Если они трясутся синхронно, веревка может образовывать регулярную структуру волн, колеблющихся вверх и вниз, с неподвижными точками вдоль веревки, где веревка почти неподвижна (узлы), и точками, где дуга веревки максимальна (пучности).
Акустический резонанс
Гексагональное облако на северном полюсе Сатурна первоначально предполагалось, что он стоит Россби волны. Однако в последнее время это объяснение оспаривается.
Стоячие волны также наблюдаются в физических средах, таких как струны и столбы воздуха. Любые волны, движущиеся по среде, будут отражаться назад, когда достигнут конца. Этот эффект наиболее заметен на музыкальных инструментах, где при различных кратных вибрирующая струна или же столб воздухас собственная частотасоздается стоячая волна, позволяющая гармоники быть идентифицированным. Узлы возникают на фиксированных концах, а анузлы — на открытых. Если зафиксирован только на одном конце, доступны только гармоники с нечетными номерами. На открытом конце трубы противоузел не будет точно на конце, поскольку он изменяется из-за его контакта с воздухом, и поэтому конец исправления используется для его точного размещения. Плотность струны влияет на частоту, на которой будут воспроизводиться гармоники; чем больше плотность, тем ниже должна быть частота для создания стоячей волны той же гармоники.
Видимый свет
Стоячие волны также наблюдаются в оптических средах, таких как оптические волноводы и оптические резонаторы. Лазеры использовать оптические резонаторы в виде пары зеркал заднего вида, составляющих Интерферометр Фабри – Перо. В получить средний в полости (например, кристалл) излучает свет связно, возбуждающие стоячие волны света в полости. Длина волны света очень короткая (в диапазоне нанометры, 10−9 м), поэтому стоячие волны имеют микроскопические размеры. Одно из применений стоячих световых волн — измерение малых расстояний с помощью оптические балки.
Рентгеновские лучи
Вмешательство между рентгеновский снимок балки могут образовывать Стоячая волна рентгеновского излучения (XSW) поле. Из-за короткой длины волны рентгеновского излучения (менее 1 нанометра) это явление можно использовать для измерения событий атомного масштаба в материале. поверхности. XSW генерируется в области, где рентгеновский луч мешает дифрагированный луч из почти идеального монокристалл поверхность или отражение от Рентгеновское зеркало. Настраивая геометрию кристалла или длину волны рентгеновского излучения, XSW может перемещаться в пространстве, вызывая сдвиг в Рентгеновская флуоресценция или же фотоэлектрон выход из атомов у поверхности. Этот сдвиг может быть проанализирован, чтобы точно определить местоположение определенного атомного вида относительно нижележащего Кристальная структура или зеркальная поверхность. Метод XSW использовался для уточнения деталей атомарного масштаба. присадки в полупроводниках, атомный и молекулярный адсорбция на поверхностях, и химические превращения, связанные с катализ.
Механические волны
Каякеры, серфинг стоячая волна в Национальный парк Грейт-Фолс.
Стоячие волны можно механически вызвать в твердую среду с помощью резонанса. Один простой для понимания пример — это два человека, которые трясут оба конца скакалки. Если они трясутся синхронно, веревка будет образовывать регулярный узор с узлами и пучностями и будет казаться неподвижной, отсюда и название стоячей волны. Точно так же консольная балка может иметь стоячую волну, наложенную на нее путем применения базового возбуждения. В этом случае свободный конец перемещается вбок на наибольшее расстояние по сравнению с любым местом вдоль балки. Такое устройство можно использовать как датчик отслеживать изменения в частота или же фаза резонанса волокна. Одно приложение — это измерительное устройство для метрология размеров.
Волны Фарадея
В Волна Фарадея представляет собой нелинейную стоячую волну на границе раздела воздух-жидкость, вызванную гидродинамической неустойчивостью. Его можно использовать в качестве шаблона на жидкой основе для сборки микромасштабных материалов.
Физика — Поурочные планы к учебникам Мякишева Г. Я. и Касьянова В. А. 11 класс
Стоячие волны — Механические волны — Колебания и волны
Цель: сформировать понятие стоячей волны.
Ход урока
I. Организационный момент
II. Повторение
1. Вопросы для повторения.
— Какая волна называется гармонической?
— Объясните возникновение сжатия и растяжения в продольных гармонических волнах.
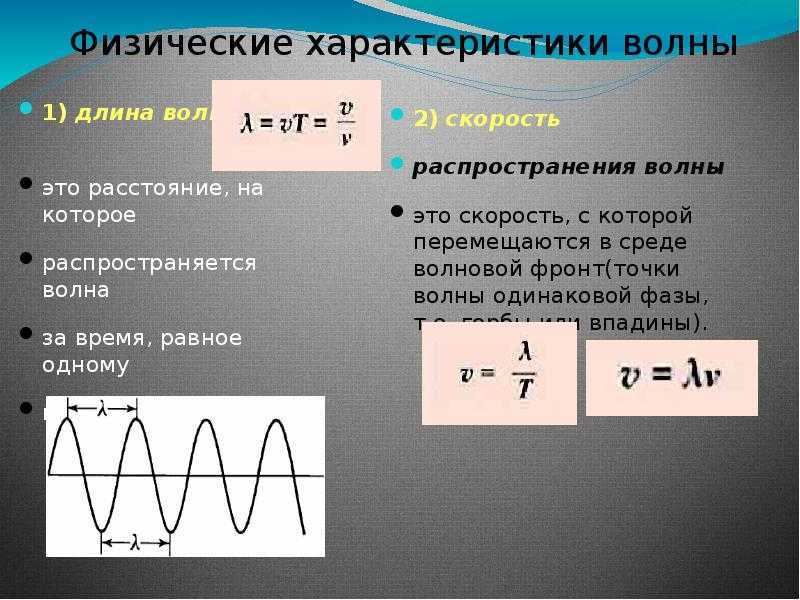
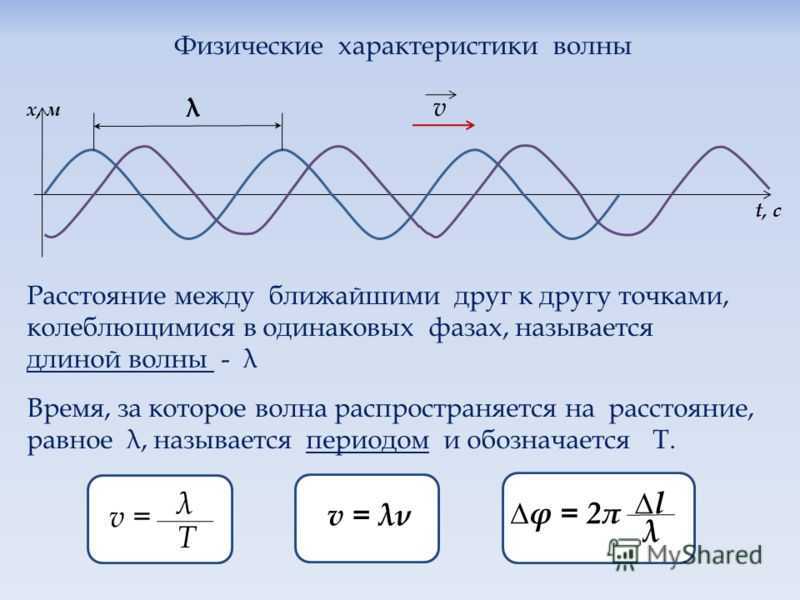
— Что такое длина волны?
— По какой формуле вычисляется длина волны?
— В чем суть поляризации?
— Как определяется плоскость поляризации?
2. Фронтальная работа с классом.
Фронтальная лабораторная работа № 1 «Исследование отражения плоских волн»
Ход работы
Установите кювету с возбудителем плоской волны и стробоскопом. Поместите в кювету металлический брусок для отражения волн. Вы должны увидеть возникновение волн. Заметьте, что эти волны отражаются как плоские волны.
Положите лист белой бумаги на экран и зарисуйте эти волны, отметьте углы падения и отражения. Таким способом вы сможете убедиться, что угол падения волны равен углу ее отражения.
Фронтальная лабораторная работа № 2 «Исследование отражения сферических волн»
Ход работы
Замените возбудитель плоской волны шариком для образования сферических волн.
После отражения плоским отражателем волны имеют сферическую форму. Центром этих сферических волн будет точка, расположенная на том же расстоянии позади отражателя, как и волнообразователь перед отражателем. Это указывает на то, что расстояние до «изображения» позади отражателя равно расстоянию до предмета перед отражателем.
III. Изучение нового материала
Опыт: Возьмем резиновый шнур, один конец которого закреплен к стене. Взмахнув раз рукой, пошлем единичный импульс. По шнуру побежит волна, и, достигнув стенки, будет от нее отражаться.
В результате на любом участке шнура встречаются две волны, бегущие в противоположные стороны. Вызванные ими колебания складываются. Частоты этих колебаний одинаковы, а амплитуды почти одинаковые, затухание колебаний вдоль шнура не велико, но фазы их различны. Бегущая (незатухающая) волна и отраженная проходят различные пути по данному участку шнура. В результате амплитуда удваивается. Такие точки называются кучностями. Если в какой-нибудь точке складывать колебания с противоположными фазами, то точка остается в покое. Такие точки называются узлами. Узлы и кучности не перемещаются вдоль шнура. В результате распределение смещения точек шнура относительно их положений равновесия в любой момент времени образует волну, которая не перемещается в пространстве. Такая волна называется стоячей волной. Расстояние между соседними узлами (или кучностями) равно половине длины волны. В стоячей волне в среднем по времени не происходит переноса энергии. Энергия волны между двумя узлами остается неизменной. Совершается только превращение кинетической энергии в потенциальную и наоборот.
Стоячие волны могут получаться в телах любой формы, а не только в таких сильно удлиненных телах, как струна или шнур. Неподвижные места стоячей волны — ее узлы — представляют собой поверхности, рассекающие объем тела на участки, в середине которых наиболее сильные колебания.
Опыт: Хладниевые фигуры
Пластинку из дерева или стекла закрепляют к одной точке и засыпают песком. По краю проводят смычком, натертым канифолью. Песок сбрасывается с кучностей и собирается на узловых линиях. Вид фигур зависит от формы пластинки и места скрепленной точки, в какой месте проводить смычком, и где придерживать пластинку пальцами.
IV. Решение задач
Р — 435; Р — 438.
V. Подведение итогов урока
Домашнее задание
Р — 440; Р — 439.
ПредыдущаяСледующая
Коэффициент стоячей волны, фаза и передача энергии
Если две движущиеся в противоположных направлениях бегущие волны имеют разную амплитуду, они не будут полностью подавляться в узлах, точках, где волны сдвинуты по фазе на 180 °, поэтому амплитуда стоячей волны не будет равна нулю в узлах, но это всего лишь минимум. Коэффициент стоячей волны (КСВ) — это отношение амплитуды в пучности (максимум) к амплитуде в узле (минимум). Чистая стоячая волна будет иметь бесконечный КСВ. У него также будет постоянная фаза в любой точке пространства (но он может поворачиваться на 180 ° каждые полцикла). Конечный ненулевой КСВ указывает на то, что волна является частично стационарной и частично бегущей. Такие волны можно разложить на суперпозиция двух волн: составляющей бегущей волны и составляющей стационарной волны. КСВ, равный единице, означает, что волна не имеет стационарного компонента — это чисто бегущая волна, поскольку отношение амплитуд равно 1.
Чистая стоячая волна не передает энергию от источника к месту назначения. Однако волна по-прежнему подвержена потерям в среде. Такие потери будут проявляться в виде конечного КСВ, указывая на то, что компонент бегущей волны покидает источник, чтобы восполнить потери. Даже несмотря на то, что КСВ теперь конечен, все же может случиться так, что энергия не достигает места назначения, потому что движущийся компонент просто обеспечивает потери. Однако в среде без потерь конечный КСВ подразумевает определенную передачу энергии к месту назначения.
Гармоники (флажолеты) в музыке
Композиторы часто применяют гармоники/флажолеты на струнных инструментах, при этом наиболее часто используют «четвертую касательную». Одним пальцем музыкант зажимает струну, получая ноту за счет отрезка определенной длины, а другим легко касается струны там, где располагается нота на 4 тона выше (отсюда и название). Данная точка лежит на четверти длины отрезка струны, поэтому образуется 4-я гармоника базовой частоты в четыре раза больше базовой, т.е. получается интервал в две октавы. Струнные гармоники/флажолеты называются «натуральными» если они образованы от открытых струн и «искусственными» если струна прижимается. Ниже на рисунке показано, как берется натуральный флажолет. Для наглядности рисунок вытянут по вертикали.
![]()
Прослушайте фрагмент. Сначала звучит открытая струна А(ля), затем ее четвертая касательная (4-я гармоника).
Так обозначается на нотном стане «четвертая касательная» на скрипичной струне А(ля)
Стоячая волна
Иногда кажется, что волны вместо движения вибрируют. Подобные явления формируются из-за наложения двух или больше перемещающихся в разных направлениях волн. Помехи складываются по мере прохождения. Если обладают схожей амплитудой и длиной, то заметно чередование конструктивных и деструктивных помех. В результате получаем стоячую волну.
Отображена как сумма двух распространяющихся волн, перемещающихся в противоположных направлениях (красный и синий)
Стоячие волны можно найти в струнах музыкальных инструментов. Узлы – точки, лишенные перемещения. То есть, это определенная позиция, где волновое возмущение приравнивается к нулю. Фиксированные концы также выступают узлами, потому что струна туда не способна двигаться. Пучность указывает позицию максимальной амплитуды в стоячей волне.
У стоячей волны есть частота, связанная со скоростью распространения возмущения в струне. Длина волны (λ) вычисляется по дистанции между точками, где струна зафиксирована на позиции.
![]()
Здесь вы видите главный режим и первые шесть обертонов
Наиболее низкая частота – основная и выступает самой длинной. Обертоны или гармоники кратны основной частоте.
ОЧЕВИДНЫЕ РЕШЕНИЯ ЧЕРЕЗ ГЕОМЕТРИЮ
Допускать наличие стоячих волн не разумно в виду их патогенного воздействия, но этот вопрос решаем, так что начнем с самого простого и понятного метода для архитектуры. С точки зрения механики и геометрии, для остановки зацикленного рикошета между двумя плоскостями можно изменить угол поворота или наклона одной из них, грубо, но эффективно. Таким образом волна уйдет совершенно в другую сторону и не будет задерживаться в помещении, также возможно ее гашение
Важно именно изменить положение конструкции, а не создать на ней обшивку под углом из более легкого материала, такой способ не сработает. Хотя возможно есть мощные отражатели легкого веса или малой толщины, но эта область мало исследована
Поэтому надежнее всего использовать цельную, основную конструкцию. Будем считать это первым решением.
Вторым геометрическим решением является изменение плоской и ровной формы одной или нескольких стен, а также возможно потолка на криволинейную. Волнистая, вогнутая или выгнутая поверхность уже не способна создать волну, которая войдет в замкнуты цикл столкновения и складывания с противоположными волнами. Идеальным решением в этом методе будет применение круглой, овальной и подобным им формам стен в плане. Купол в этом отношении – это весьма эффективное решение, так как в нем постоянно меняется угол наклона и поворота. В общем любое искажение параллельных плоскостей сбивает стоячую волну. Но самое изящное решение в этом методе будет искажение формы, на подобии энтазиса античных колонн. На основе этого приема построены почти все храмы на территории современной Греции. В них нет прямых линий, все конструкции являются симметричными или ассиметричными дугами, не заметными глазу.
Третьим способом избавиться от стоячих волн назовем метод дробления. В этом случае стены и потолок могут оставаться прямыми и перпендикулярными, но на них появляются выступы и углубления. Их роль исполняют пилястры, колонны, полуколонны, ниши, эркеры, барельефы и множество других вещей. Это сравнимо с ездой по ровной асфальтовой дороге и по грунтовой или вовсе по бездорожью. Во втором случае скорость существенно снижается и существует вероятность вовсе застрять. Так и наши волны, уже не могут без усилий перемещаться от одной ровной плоскости к другой. Кстати бревенчатая, не выровненная стена и другие сильно рельефные поверхности обладают подобными свойствами.
Эффективность и объективность применения данных методов устранения стоячих волн различны, но в любом случае все они работоспособны и самое главное – применялись в прошлом. Хотя это всего лишь одно из множества результатов, достигаемое использованием вышеописанных приемов. Следует подметить, что не каждое современное помещение имеет стоячие волны, так как для их возникновение необходимо резонансное расстояние, которое иногда может не давать активного эффекта, на этом принципе основан отдельный метод. Кстати, с точки зрения эниологии в полностью симметричном помещении, например, в квадратном, стоячих волн не существует, они сжимаются в одну точку посередине, это доказуемо и реально, но не будем пока касаться этой темы.
Немного технической информации для струнников
Несмотря на то, что «четвертая касательная» наиболее часто встречающийся флажолет, это не вполне удачный пример, поскольку получить четвертую гармонику гораздо проще, нежели «две четверки». Как известно, касание струны на отрезке 1/n (где n — целое число) дает n-ую гармонику, и для низких гармоник правило соблюдается, но для высших гармоник особое значение играет толщина струны, и здесь формула перестает работать. Таким образом, гармоники выше 8-й практически не берутся.
Если взять на струне подряд пять полутонов, то мы получим точку, соответствующую 1/3 длины струны, то есть «пятая касательная» даст нам третью гармонику. Гармоники расположены в следующем порядке:
| интервал на грифе | часть струны | номер гармоники | интервал от базовой ноты |
| октава | 1/2 | 2 | октава |
| квинта | 1/3 | 3 | октава + квинта (дуодецима) |
| кварта | 1/4 | 4 | две октавы |
| большая терция | 1/5 | 5 | 2 октавы + б. терция |
| малая терция | 1/6 | 6 | 2 октавы + квинта |
| ув. кварта | 2/7 | 7 | 2 октавы + м. секста повышенная |
| малая секста | 3/8 | 8 | 3 октавы |
| большая секунда | 1/9 | 9 | 3 октавы + б. секунда |
Положения нот звукоряда соответствуют чистому строю. Касание струны на 2/9 ее длины предпочтительней, чем на 1/9, хотя данная точка расположена не над нотой гаммы, а немного выше малой терции. Буду рад, если альтисты или виолончелисты исполняющие «Практикующая бесконечность» Радулески (Radulescu’s «Practicing Infinity») пришлют мне свои предложения о способах исполнения высоких флажолетов.
Несовершенство настройки по гармоникам (флажолетам)
Есть несколько проблем при настройке любой гитары, в том числе при использовании флажолетов, о чем говорилось выше. Приблизительность настройки инструмента очевидно связана с равномерной темперацией. Даже если бы струны были идеальны, а положение ладов на грифе идеально отвечало равномерной темперации, при настройке по четвертой гармонике струн E-A (ми-ля), и A-D (ля-ре), октава между открытой нижней E(ми) и нотой ми на 2-м ладу струны D(ре) отклонялась бы приблизительно на 4 цента ((4/3)222/12=1.996), что приводило бы к появлению одного интерференционного биения в несколько секунд.
Другая проблема заключается в том, что в зоне верхнего порожка и подставки струны не могут обеспечить абсолютную гибкость (что было отмечено выше). В результате 1-й обертон на струне всегда будет чуть выше октавы, второй выше чем дуодецима (октава + квинта), и так далее. Так настройка в унисон 4-ой «гармоники» струны Е(ми) и 3-ей гармоники струны А(ля) при сравнении открытых струн даст интервал несколько больший, чем кварта, отчего приходится исправлять настройку, чтобы иметь равномерную темперацию.
Еще один отрицательный момент относится к расположению ладов и подставки. При прижиме струны на двенадцатом ладу увеличивается и ее длина (это уже не самое короткое расстояние между верхним порожком и подставкой), и ее натяжение. Вследствие этого, а также из-за выгиба конца струны, будь 12-й лад точно посередине между верхним порожком и подставкой, мы бы имели интервал больше октавы. Поэтому расстояние от подставки до 12-ого лада делают несколько большим, чем до верхнего порожка. Необходимо отметить, что в зависимости от вида струн эффект может быть различен. На электрогитарах есть возможность регулировать положение каждой подставки струны, на некоторых гитарах подставку поворачивают под углом, а в случае с классической гитарой прямая подставка ведет к определенному компромиссу в настройке.
Вышеописанные моменты сложно отследить с большой точностью, поскольку при анализе звука струны, возбуждаемой щипком, неточности составляют лишь несколько центов, что не намного больше разрешающей способности слуха или приборов настройки. Настройка колками также не позволяет достичь точности менее двух центов. С другой стороны, если Вам удастся интонировать мелодию с точностью в пределах двух центов, это будет большая удача — большинству музыкантов такое не по силам!
Определенная часть проблем настройки касается старения струн. Там, где Вы касаетесь их пальцами левой руки, они вбирают в себя пот и становятся более тяжелыми (хотя может иметь место и износ материала в местах, которые трутся об лады). Струны также изнашиваются под пальцами правой руки. Неоднородность струн ведет к невозможности их точной настройки. Мойка струн может помочь лишь отчасти.
Конечно, на безладовом инструменте большинство этих проблем можно обойти, но аккордная техника при этом сильно страдает.
![]()
На рисунке показаны гармоники открытой струны СОЛЬ контрабаса или виолончели. (Ноты для контрабаса записываются октавой выше его звучания.) Над нотами указаны номера гармоник, а под ними записаны приблизительные частоты в Герцах, причем для наглядности сделано округление чисел. Данный пример демонстрирует закон изменения высотности гармоник, и, хотя реальные частоты составляют пропорционально несколько меньшие значения, динамика возрастания частот от значения в 100Гц отражена абсолютно точно. (Приведенные значения частоты ноты СОЛЬ и ее гармоник могли бы иметь место при камертоне Ля=449Гц. Примечание переводчика).
Перепечатка статьи возможна только с согласия автора Джо Вулфи J.Wolfe()unsw.edu.au, а также фирмы ГОСПОДИН МУЗЫКАНТ, осуществлявшей ее перевод.
2002






![Коэффициент-стоячей-волны [сайт патологического холостяка]](http://basis-tp.ru/wp-content/uploads/6/d/3/6d38f391ae8d4fd228cf021246bad3d4.jpeg)